В этом разделе вы найдете информацию о том, как рассчитать лестницу, определить ее параметры, определить размер лестницы и составить проект.
Выбрав тип и размер лестницы и место ее расположения в дома, можно приступать к определению ее параметров. Это количество маршей, полезная ширина деревянных лестниц, размер винтовой лестницы, длина горизонтального заложения каждого марша, количество и длина лестничных площадок, угол наклона лестниц.
Если по поворотной или круговой лестнице предполагается переносить крупногабаритную неразборную мебель или другие вещи, полезную ширину марша S, (для лестницы с промежуточной лестничной площадкой Рис. 13) поможет определить формула расчета лестницы:
где: d - длина предмета; m - ширина предмета. Для одномаршевых поворотных (рис. 14) и круговых лестниц (т. е. для лестниц с забежными ступенями) от габаритов переносимых предметов зависят не только ширина марша, но и величина внутреннего радиуса его закругления (Rвн). Чем она больше, тем шире и длиннее может быть переносимый по лестнице предмет. Величину этого радиуса можно определить по формуле расчета лестницы:
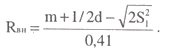
При этом к расчетным величинам ширины марша и радиуса его закругления при определении размера лестницы обязательно нужно добавлять не менее 10 см, которые необходимы для возможности поворотных маневров с переносимыми предметами.
Количество маршей в лестнице (размер лестницы любой) зависит:
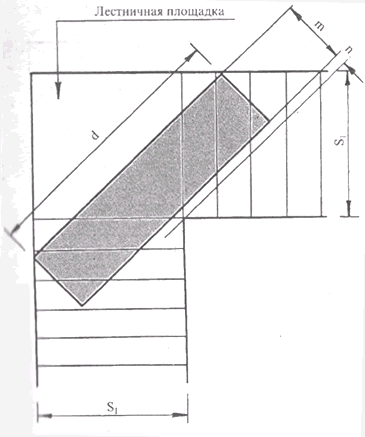
Рис 13. Схема расчета лестницы (размер лестницы любой) с промежуточной площадкой в зависимости от предполагаемых габаритов переносимого груза.
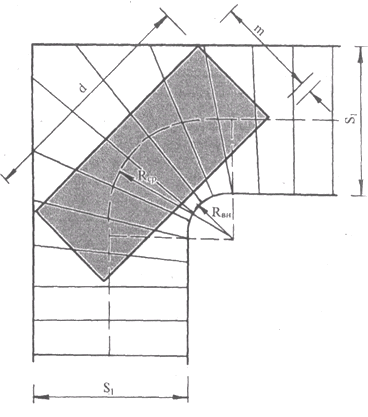
Рис. 14. Схема расчета размера лестницы (одномаршевой поворотной) в зависимости от предполагаемых габаритов переносимого груза
Параметры марша при определении размера лестницы определяются уровнем его уклона, длиной горизонтального заложения, размером и количеством ступеней в нем и зависят от двух условий:
Удобной считается лестница, подъем и спуск по которой осуществляется с наименьшими физическими усилиями и наименьшими энергетическими затратами. Другими словами, вы должны идти по ступенькам лестницы естественным шагом, не семеня и не растягивая его, не поднимая слишком высоко ноги при подъеме и не слишком сильно сгибая их в коленях при спуске.
Делая расчеты параметров (размера) лестницы, удобной для ходьбы, за исходную величину принимается уклон марша, который должен быть в пределах 1:2-1:1,75. Эти величины установлены по соотношению максимальной высоты удобного подъема ноги при движении по вертикали (30-32 см) к средней длине шага человека (60 64 см). Т. к. при передвижении по наклонной лестнице длина шага распределяется между двумя ступенями, то и нормальная, естественная, а значит, удобная ширина их принимается в пределах половины шага, примерно 30 см. Естественно, Что при движении по наклонной лестнице высота удобного подъема ноги те, чем при движении по вертикальной. Поэтому для удобных наклонных лестниц расчетная высота подъема не должна быть примерно в два раза меньше, чем для вертикальных, т. е. размер лестницы по этому критерию 15-16 см.
Уклон марша, а следовательно, и всей лестницы определяется отношением его высоты к длине горизонтального заложения.
Зная уклон и высоту марша (h), определяем длину его горизонтального заложения (/). Допустим, мы приняли уклон марша, равный 1:2. Тогда длина его заложения определится по формуле:
где у - знаменатель относительной величины принятого уклона марша. Определив таким образом длину заложения, рассчитываем количество ступеней в марше, помня при этом, что крайняя верхняя проступь марша совпадает с верхней лестничной площадкой Обозначим ширину ступени при вычислении размера лестницы символом b (рис. 9), количество ступеней символом х, а длину заложения символом /. Очевидно, что:
Разделив высоту марша на количество ступеней получим высоту ступени - а (рис. 9):
Замечания: 1. При расчете такого параметра размера лестницы как количество ступеней по формуле (3) во внимание принимается ширин: ступени, определяемая расстоянием между внешними крайними точками ступени, но никак не ширина ее проступи, которая может отличаться от ширины ступени на величину выступа (рис. 9). 2. Нетрудно заметить, что соотношение высоты и ширины ступени, как и отношение высоты марша к длине его горизонтального заложения, является показателем уклона марша, т.е.
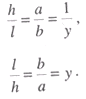 (5-6)
(5-6)
Если при расчете параметров (размера) лестницы вы хотите, чтобы она занимала минимум площади, за исходные величины примите допустимый максимальный уклон марша (1:1 - для лестниц, ведущих в жилые помещения и 1:0,85 для лестниц, ведущих в нежилые помещения) и допустимую по соображениям безопасности минимальную ширину ступени (200 мм). Высота ступени в этом случае, согласно формулам (2) и (5) равна:
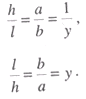 (7)
(7)
Где y - знаменатель относительной величины уклона марша. Тогда длина горизонтального заложения марша
Как видно из формулы (6), показателем удобности по размеру лестницы мы может служить коэффициент отношения ширины ступени к ее высоте, называемый также коэффициентом уклона марша:
При ширине ступени от 26 до 30 см и величине коэффициента в пределах от 1,75 до 2 лестница считается удобной. Такой же считается лестница с отношением ширины ступени к ее высоте как 30/15 (к=2), 31/16 (k=1,94) и 29/17 (k=1,70). Последнее соотношение (формула расчета лестницы) считается идеальным для домовых лестниц. Рекомендуемые соотношения ширины ступени к ее высоте приведены в табл.1. Особенности расчета маршей с забежными ступенями. Расчет параметров поворотных лестниц (размера лестниц) с забежными
Таблица 1. Рекомендуемые отношения ширины ступени к ее высоте:
| Отношение ширины ступени к ее высоте | Коэффициент уклона | Угол подъема марша в градусах |
| 37/14 | 2,64 | 20,8 |
| 30/12 | 2,50 | 21,8 |
| 35/15 | 2,33 | 23,2 |
| 30/15 | 2,00 | 26,6 |
| 31/16 | 1,93 | 27,4 |
| 29/17 | 1,70 | 30,5 |
| 28/17,5 | 1,60 | 32,0 |
| 27/18 | 1,50 | 33,7 |
| 26/19 | 1,36 | 36,3 |
| 23/20 | 1,15 | 41,0 |
| 21/21 | 1,00 | 45,0 |
| 20/23 | 0,85 | 49,6 |
ступенями выполняется несколько иначе. Здесь уже необходимо оперировать такими понятиями, как средняя линия марша, радиус закругления средней линии и угол поворота марша.
Средняя линия марша при определении размера лестницы - это воображаемая линия, которая на прямых участках марша проходит строго по его середине, а на криволинейных - по линии, параллельной внутреннему краю марша, на расстоянии равном половине его ширины. В тех случаях, когда на поворотах внутренний край марша представляет собой круговую кривую, средняя линия параллельной ей круговой кривой (см. примеры на рис. 15 и 16). Центры окружностей обеих кривых в таких случаях совпадают, и те, кто еще не забыл начисто школьный курс геометрии, знают, что эти дуги являются частями концентрических окружностей. В иных же случаях средняя линия на повороте та является ломаной кривой.
Величина радиуса закругления средней линии зависит радиуса вписанной между маршами воображаемой окружности и от полезной ширины марша. Величина радиуса воображаемой окружности, вписанной между внутренними краями поворотного марша, для поворотных лестниц принимается равной 3050 см определяется расчетом по габаритам предполагаемых к переносу по лестнице предметов обстановки и оборудования.
Угол поворота марша - это угол, образованный на горизонтальной проекции лестницы между створами внешних граней первой и последней ступеней марша.
Особенности расчета маршей с забежными ступенями (размер лестницы) заключаются, во-первых, в несколько иных методиках расчета габаритов горизонтальной проекции зависящих от типа лестницы, и, во-вторых – в раскладке и определении размеров ступеней на его криволинейных участках.
Наиболее характерными для иллюстрации особенностей расчета маршей с забежными ступенями являются четвертьоборотные, полуоборотные и винтовые одномаршевые лестницы.
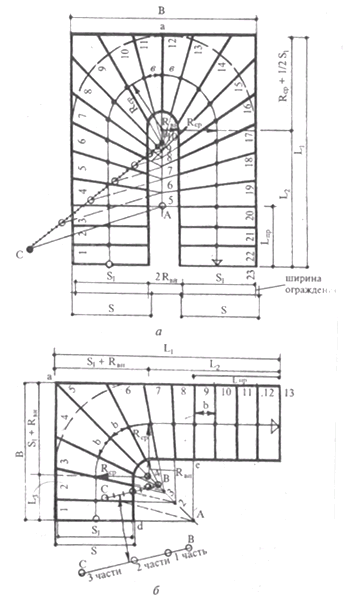
Рис. 15. Методы пропорциональной разбивки: а - полуоборотного марша; б - четвертьоборотного марша
Замечание
1. Ширина забежных ступеней (размер лестницы) определяется по средней линии и должна быть, как и ширина прямых ступеней, постоянной величиной на всем протяжении лестницы. В тех случаях, когда средняя линия является воображаемой круговой кривой, ширина ступеней определяется по хордам, соединяющим точки пересечения средней линии с горизонтальными проекциями граней ступеней.
2. Ширина марша в пределах криволинейного участка лестницы принимается по направлению радиуса средней линии.
3. Длина горизонтального заложения поворотного или кругового марша при определении размера лестницы определяется также по средней линии.
Расчет габаритов горизонтальной проекции четвертьоборотного марша (рис. 15б).
Имеем: полезную ширину марша S1; угол поворота марша ά = 90; ширину ступени b; длину горизонтальной проекции наружного края марша /1 от последней ступени до вершины угла поворота марша (задается по условиям планировки лестницы, например, по имеющемуся расстоянию, в которое надо вписать лестницу между краем лестничной площадки в конце марша и стеной); радиус кривой Rвн вписанной между внутренними краями называемой далее «внутренним радиусом».
Определяем: длины /2, /3 горизонтальных проекций на участках от его крайних ступеней до начала "криволинейной средней линии и длину горизонтальной проекции B наружного края марша от первой ступени до вершины угла поворота. Эти данные необходимы для того, чтобы встроить лестницу в отведенное место. Формула расчета лестницы в этом случае такова:
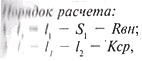
где Kcp - длина средней линии на кривой, равная
Расчет габаритов горизонтальной проекции полу оборотного марша (рис. 15а).
Имеем: Те же данные, что и в предыдущем примере:
Порядок расчета:
где Kcp - длина средней линии на кривой, равная πRcp
Расчет габаритов горизонтальной проекции винтового марша (рис. 16).
Имеем: угол поворота марша ά; полезную ширит марша S1; длину горизонтальной проекции средней линии марша lcp = Kcp (а значит - количество ступеней x, ширину ступени bcp по средней линии марша и высоту ступени a).
Определяем: радиус средней линии Rcp; радиус кривой, вписанной между внутренними краями марша Rвн; радиус кривой, описанной по наружному краю марша Rн, расстояние в плане B между наружным и краями марша; ширину узкого (внутреннего) края ступени bвн, которая должна быть не менее 10 см.
Порядок расчета (рис. 16 г):

Замечание. Если по винтовой лестнице предполагается переносить предметы определенных размеров, необходимую для этого ширину марша по заданным длине d, ширине m предмета и радиусу внутренней кривой Rвн можно рассчитать по формуле:
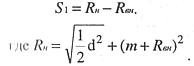
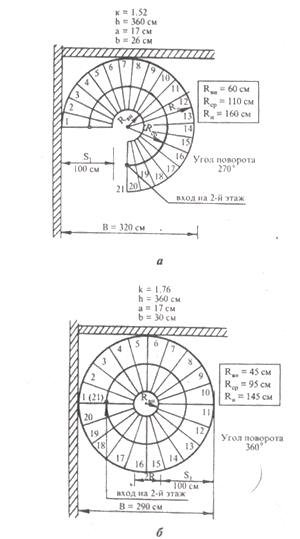
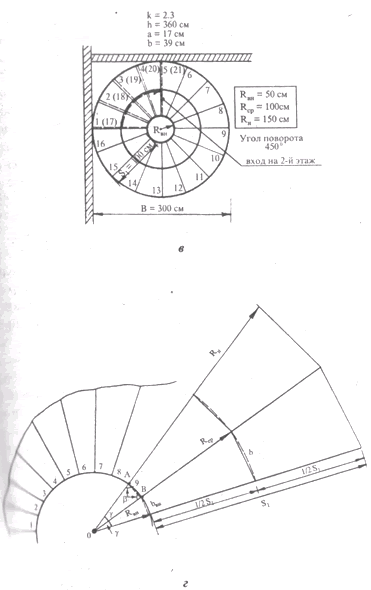
Рис. 16. Примеры расчета габаритов горизонтальной проекции винтового марша: а - с углом поворота 270°; б - с углом поворота 360°; в углом поворота 450°; г - фрагмент плана марша с обозначением расчетных элементов.
Раскладка и определение размера ступеней (размер лестницы). Чтобы ходьба по криволинейному маршу была максимально приближена к ходьбе по прямому, а на переходе с прямолинейного участка на криволинейный у человека не возникало ощущения резкого изменения темпа и направления шага, угол поворота марша (угол наклона лестниц) должен быть распределен между как можно большим количеством забежных ступеней, а углы поворота ступеней плавно нарастать от входа на криволинейные; участок до его середины и уменьшаться от нее до выхода из криволинейного участка. Разумеется, при таких условиях размеры забежных ступеней будут отличаться друг от друга. Этот принцип устройств забежных ступеней не распространяется, однако, ни винтовые лестницы, все ступени в которых должны быть абсолютно одинаковыми по размерам и форме Но винтовые лестницы и не считаются удобными и сооружаются обычно только в стесненных планировочных условиях.
Важно
1. Забежные ступени можно располагать и вне криволинейного участка средней линии, что делает поворот более плавным. Чем больше забежных ступеней находится на прямых участках средней линии, тем удобнее передвижение по лестнице.)
2. Ширину забежных ступеней (bcp) определяют по средней линии. Она должна быть равна ширине прямых ступеней (b).
Точный математический расчет размеров и положения забежных ступеней четвертьоборотных и оборотных лестниц относительно средней линии марша (как рассчитать лестницу) довольно утомителен и сложен. Поэтому на практике прибегают к раскладке забежных ступеней при помощи разных графических способов. Наиболее употребительными являются метод пропорциональной разбивки и метод полуокружности. И первый, и второй применимы для обоих упомянутых типов поворотных лестниц, но предполагают разный принцип раскладки ступеней относительно линии, делящей угол поворота марша пополам (биссектрисы).
Важно. При разбивке методом полуокружности располагать на биссектрисе угла поворота ось одной из забежных ступеней, а при методе пропорциональной разбивки наружную грань одной из ступеней.
Раскладка ступеней обоими методами производится на плане горизонтальной проекции лестницы, вычерченном строго по расчетным габаритам марша в соответствии с приведенными выше методиками. План составляется на специальной бумаге с нанесенной типографским способом координатной сеткой (миллиметровке) в произвольном масштабе, позволяющем, достаточно точно отложить, например, ширину ступени. Подходящим для этого является масштаб 1:10, при котором 1 - единица длины отрезка на плане соответствует 10 единицам этого же отрезка в натуре. Перед тем как начать раскладку забежных ступеней, на план марша наносят среднюю линию и ось симметрии, которая для четвертьоборотной лестницы проводится из вершины угла поворота марша через центр круговой средней линии, а для полуоборотной - через центр кривой и точку, разделяющую торцевой наружный край марша на два равных отрезка. После этого можно приступать к раскладке забежных ступеней одним из указанных методов.
Метод пропорциональной разбивки (рис. 15). Обе части средней линии марша, разделенные его осью симметрии, разбивают, начиная от оси симметрии, на отрезки, соответствующие ширине ступени. Общее количество полученных таким образом отрезков должно быть, само собой разумеется, равным расчетному количеству ступеней в марше минус единица. Затем определяют начало и конец участка марша, в пределах которого будут находиться забежные ступени, то есть определяют количество прямых ступеней и начале и в конце марша.
Важно. Пограничные прямые ступени на противоположных концах забежного участка располагать на одинаковом расстоянии от вершины угла поворота марша.
Пограничные ступени соединяют друг с другое прямой (для полуоборотных маршей) или ломаной линией (для четвертьоборотных маршей), образующих в обоих случаях угол поворота марша (см. рис. 15а ) для первого случая и рис. 156 для второго). при пересечении этой линии с осью симметрии марша получают одну из точек (в нашем примере - точку являющихся исходными для раскладки забежных пеней.
Далее по оси симметрии марша в пределах строительной ширины откладывают прямую линию. Она принимается как проекция наружной грани одной из ступеней (на рис. 15а - 12й ступени, на рис. 15б 5й). Через ближайшую к этой грани отметку на средней линии, которая обозначает ширину ступени, находящейся слева или справа (в нашем случае слева), проводят линию. Она пересекает марш от его наружного края до его симметрии под произвольно острым углом. Эта линия в пределах наружного и внутреннего краев марша будет являться проекцией грани ступени, находящейся непосредственно слева или справа перед осью симметрии марша (в примерах рис. 15 это ступень 11 или 5).
Важно.
1. При выборе положения этой ступени не забывать о соблюдении требования СНиПа относительно ширины узкого торца забежной ступени, которая должна быть не менее 10см.
2. Положение этой ступени является исходным для раскладки предыдущих забежных ступеней: чем больше выбранная ширина ее узкого торца, тем менее плавным будет переход от прямого движения по лестнице к криволинейному.
Отрезок между точкой пересечения указанной с осью симметрии марша (в наших примерах точка B) и точкой пересечения с осью симметрии створов граней последних прямых ступеней (точкой А) необходимо разделить на отрезки в пропорции 1:2:3:4:5:7 и т.д., концы которых будут исходными для определения положения граней остальных забежней. Разбивку этого отрезка на пропорциональные части при определении размера лестниц производят с помощью вспомогательной произвольной длины, проводимой из точки В в направлении точки А под произвольным, но непременно острым углом к оси симметрии марша в той половине марша, в которой начата разбивка забежных ступеней (в наших примерах эта половина - левая). Эту линию, начиная от точки В, разбивают на отрезки в указанной пропорции, при которой длина каждого последующего отрезка должна быть во столько раз больше исходной длины первого отрезка, во сколько раз число, обозначающее порядковый номер этого отрезка, больше числа 1, обозначающего порядковый номер первого отрезка. Количество откладываемых в таком соотношении отрезков должно соответствовать количеству забежных ступеней, предусмотренных на этой половине марша. Длина первого от точки В отрезка выбирается произвольно, длина следующего назначается в два раза большей первого длина третьего - в три раза большей и т.д. до после него, конец которого (в наших примерах - точка С) соединяется прямой линией с точкой А. Из концом промежуточных отрезков, находящихся на вспомога тельной линии между точками В и С, последовательно проводят линии, параллельные линии СА, до пересечения с отрезком ВА, находящимся на оси симметрии марша. Каждая из полученных точек пересечения (на рис. 15а - точки 5, 6, 7, 8, 9, 10, а на рис. 156 -точки 2,3,4) будет исходной для определения положений грани соответствующей ступени. То есть: первая из них после точки В (точка 10 или 5) будет предназначена для ступени (10 или 4), предшествующей уже уложенной (11 или 5). Из этих точек через точки разметок соответствующих ступеней, находящихся на средней линии по обе стороны от оси симметрии марша, проводят прямые линии. Положение этих прямых в пределах марша и определит положения наружных граней раскладываемых, забежных ступеней.
Метод полуокружности. Среднюю линию разбивают на отрезки, равные ширине ступени, таким образом чтобы на ось симметрии попала продольная ось одной из ступеней (рис. 17). Ширина этой ступени в зоне примыкания к внутреннему краю марша выбирается произвольно, но должна быть не менее 10 см (помните нормы?) и не более, разумеется, диаметра воображаемой окружности, вписанной между внутренними краями марша.
Определяется положение последних прямых ступеней, которые будут находиться перед забежным участком марша. Створы граней этих ступеней соедининяются прямой (при повороте марша на 180°) или ломанной (при повороте марша на 90°) линией.
Из точки пересечения этой линии с осью симметрии марша (на рис. 17 точка А) описывают полуокружность радиусом АВ, равным, как видно из рисунка, расстоянию между этой точкой и точкой пересечения оси симметрии с внутренним краем марша (точка В). иную полуокружность разбивают на равные количество которых соответствует количеству предусматриваемых забежных ступеней. Разбивка полуокружности ведется от точки В. О правильности и точности разбивки будет свидетельствовать симметричное положение отрезков относительно друг друга по обе от оси симметрии марша. Далее. Из концов отмеченных на полуокружности отрезков параллельно линии, соединяющей грани прямых ступеней, проводят линии до пересечения с ближайшим внутренним краем марша. Из точек пересечения этих линий с внутренним краем марша (некоторые из них помечены на рис. 17 цифрами со штриховой пометкой)
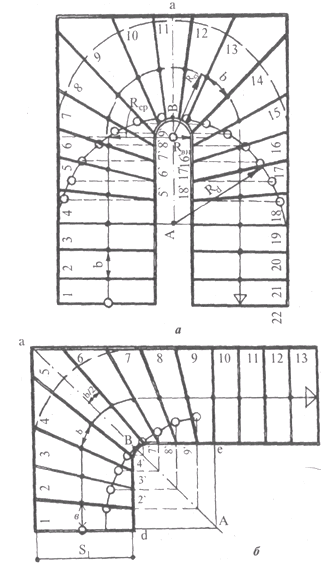
Рис. 17. Примеры раскладки забежных ступеней методом полуокружности: а - полуоборотного марша; б - четвертьоборотного марша
проводят линии через точки разметки ступеней на средней линии. Положение этих прямых в пределах марша и определит положение наружных граней раскладываемых забежных ступеней.
После того как забежные ступени разложены на плане марша одним из предложенных здесь способов, остается как можно точнее снять с чертежа размеры каждой и проверить, соответствует ли суммарная ширина их широких и узких торцов расчетным размерам соответственно наружного и внутреннего краев участка марша, на котором предусматриваются забежные ступени. Для этого необходимо рассчитать длины наружного и внутреннего краев горизонтальной проекции участка марша с забежными ступенями (из общей мины каждого края горизонтальной проекции марша вычесть суммарную ширину прямых ступеней, обозначенную на рис. 15 символом lnp) и сравнить их с суммарной шириной соответственно широких и узких торцов забежных ступеней. Полученные погрешности распределить в равных долях между всеми забежными ступенями.
В заключение довольно кропотливой, но интересной процедуры раскладки забежных ступеней графическим способом необходимо вычертить каждую из них с указанием полученных размеров лестницы (ступеней) по всем ее сторонам.